二叉树
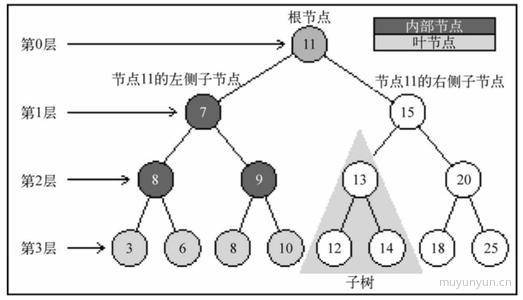
这棵树中最多有两个分支, 因此是二叉树。
根节点: 一棵树最顶部的节点内部节点: 在它上面还有其它内部节点或者叶节点的节点叶节点: 处于一棵树根部的节点子树: 由树中的内部节点和叶节点组成
概念延伸
完全二叉树(compelete binary tree):- 除了最后一行都满;
- 在最后一行不满的情况下不能只存有右子树而没有左子树;
1↙ ↘2 3↙4
满二叉树(full binary tree):- 每一行都满;
1↙ ↘2 3↙ ↘ ↙ ↘4 5 6 7
二叉搜索树(Binary Search Tree)- 左侧子节点的数字小于父节点, 右侧子节点的数字大于父节点
11↙ ↘7 15↙ ↘ ↙ ↘8 9 13 20
平衡二叉树
二叉收缩树最好的情况下查找效率是比较高, 比如上图中时间复杂度为 O(logn), 其访问性能近似于二分查找, 但最差时时间复杂度为 O(n), 如下示意:
7↘8↘9↘11↘13↘15↘20
基于此需要在二叉搜索树基础上做一下平衡,
7 8↘ 平衡后 ↙ ↘8 -------> 7 9↘9
二叉搜索树的实现
function BinarySearchTree() {function Node(key) {this.key = keythis.left = nullthis.right = null}let root = null// 插入元素// 实现思路: 至顶向下插入, 先判断顶点是否为空;顶点为空则直接在该处插入, 若不为空, 则通过比较顶点的 key 和插入元素的 key 判断该插入到顶点的左侧还是右侧, 后面进行如上递归this.insert = function(key) {const node = new Node(key)if (root === null) {root = node} else {insertNode(root, node)}function insertNode(parent, node) {if (parent.key > node.key) {if (parent.left === null) {parent.left = node} else {insertNode(parent.left, node)}} else if (parent.key < node.key) {if (parent.right === null) {parent.right = node} else {insertNode(parent.right, node)}}}}// 中序遍历this.inOrderTraverse = function(cb) {inOrderTraverse(root, cb)function inOrderTraverse(node, cb) {if (node) {inOrderTraverse(node.left, cb)cb(node.key)inOrderTraverse(node.right, cb)}}}// 先序遍历this.preOrderTraverse = function(cb) {preOrderTraverse(root, cb)function preOrderTraverse(node, cb) {if (node) {cb(node.key)preOrderTraverse(node.left, cb)preOrderTraverse(node.right, cb)}}}// 后序遍历this.postOrderTraverse = function(cb) {postOrderTraverse(root, cb)function postOrderTraverse(node, cb) {if (node) {postOrderTraverse(node.left, cb)postOrderTraverse(node.right, cb)cb(node.key)}}}// 最大值: 思路最右边this.max = function() {let maxResult = {}function getMax(node) {if (node && node.right) {maxResult = node.rightgetMax(node.right)}}getMax(root)return maxResult.key}// 最小值: 思路最左边this.min = function() {let minResult = {}function getMin(node) {if (node && node.left) {minResult = node.leftgetMin(node.left)}}getMin(root)return minResult.key}// 查找指定元素this.search = function(key) {const searchKey = function(node) {if (!node) {return false}if (key > node.key) {return searchKey(node.right)} else if (key < node.key) {return searchKey(node.left)} else {return true}}return searchKey(root)}// 移除指定 key 值this.remove = function(key) {const removeKey = function(node, key) {if (key < node.key) { // ① 如果 key 值在传入节点的左边node.left = removeKey(node.left, key)return node} else if (key > node.key) { // ② 如果 key 值在传入节点的右边node.right = removeKey(node.right, key)return node} else { // ③ 如果找到了 key 值if (node.left === null && node.right === null) { // 删除的节点为根节点node = nullreturn node}if (node.left === null) { // 删除的节点下有一个分支node = node.rightreturn node} else if (node.right === null) {node = node.leftreturn node}const minNode = findMinNode(node.right) // 删除的节点下有两个分支node.key = minNode.keynode.right = removeKey(node.right, minNode.key)return node}}// 查找最小的节点const findMinNode = function(node) {if (node.left) {return findMinNode(node.left)} else {return node}}removeKey(root, key)}}var tree = new BinarySearchTree()tree.insert(11)tree.insert(7)tree.insert(15)tree.insert(5)tree.insert(3)tree.insert(9)tree.insert(8)tree.insert(10)tree.insert(13)tree.insert(12)tree.insert(14)tree.insert(20)tree.insert(18)tree.insert(25)tree.insert(6)
三种遍历方式的不同
- 中序遍历: 可用于
二叉搜索树的排序
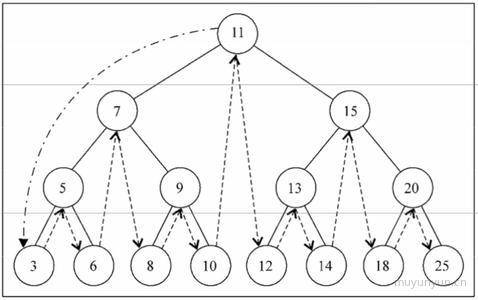
- 先序遍历: 可用于
打印结构化的文档
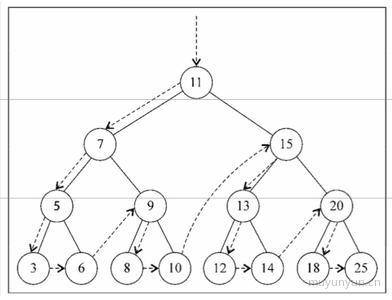
- 后序遍历: 可用于
查看文件夹目录
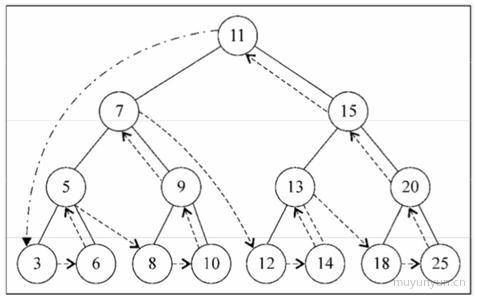
三者都为 DFS, 本质在于节点的访问时机不同。
三种遍历的实现方式大同小异, 可在上面代码中观察到实现的差异。如下是 Leetcode 中对应三种不同遍历方式的题目:
remove 的几种情况
remove 方法是二叉查找树中相对复杂的实现。思路仍然是递归。
如果要删除的 key 在传入节点的左侧, 则递归调用 removeKey(node.left, key);
如果要删除的 key 在传入节点的右侧, 则递归调用 removeKey(node.right, key);
如果要删除的 key 与传入节点相等, 有如下三种情况:
①: 删除的节点为根节点
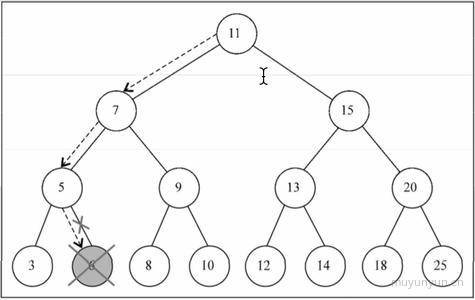
②: 删除的节点下有一个分支

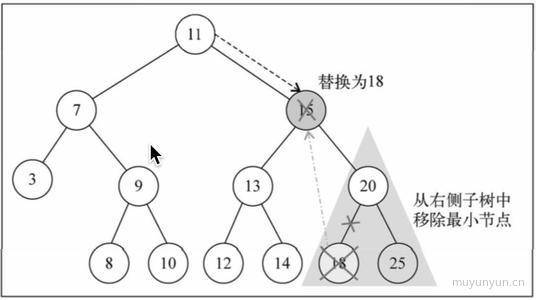
③: 删除的节点下有两个分支
这里的思路是找到当前节点的右分支中最小的节点, 然后将该节点代替当前节点, 同时移除当前节点的右分支中最小的节点
测试用例
var tree = new BinarySearchTree()tree.insert(11)tree.insert(7)tree.insert(15)tree.insert(5)tree.insert(3)tree.insert(9)tree.insert(8)tree.insert(10)tree.insert(13)tree.insert(12)tree.insert(14)tree.insert(20)tree.insert(18)tree.insert(25)tree.insert(6)var cb = (key) => console.log(key)tree.inOrderTraverse(cb) // 中序遍历: 3 5 6 7 8 9 10 11 12 13 14 15 18 20 25tree.preOrderTraverse(cb) // 先序遍历: 11 7 5 3 6 9 8 10 15 13 12 14 20 18 25tree.postOrderTraverse(cb) // 后序遍历: 3 6 5 8 10 9 7 12 14 13 18 25 20 15 11tree.max() // 25tree.max() // 3tree.search(6) // truetree.search(1) // false