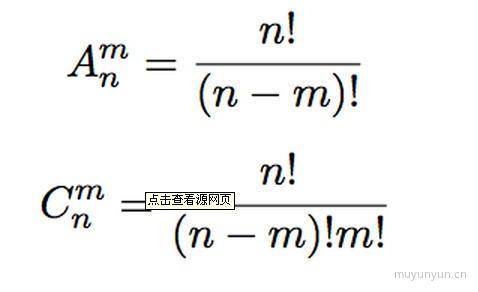一个时间复杂度的问题

有一个字符串数组, 将数组中的每一个字符串按照字母序进行排序; 然后再将整个字符串数组按照字典序进行排序; 时间复杂度是多少?

简单的复杂度分析

O(n^2)

如下是 选择排序 中的代码片段:

var chooseSort = function(arr) {
  for (let x = 0; x < arr.length; x++) {
    let min = x
    for (let y = x + 1; y < arr.length; y++) {
      if (arr[y] < arr[min]) {
        min = y
      }
    }
    let tmp = arr[x]
    arr[x] = arr[min]
    arr[min] = tmp
  }
  return arr
}

分析其时间复杂度

(n - 1) + (n - 2) + (n - 3) + ... + 0 = (n - 1 + 0) * n / 2 ≈ O(n^2)

需注意的是并不是所有有两重遍历循环的算法时间复杂度都是 O(n^2)。

function demo1(n) {
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < 30; j++) {
      ...
    }
  }
}

在 demo1 函数中, 因为内层循环的次数为常量 30, 所以其时间复杂度为 30 * n ≈ O(n)

function demo2(n) {
  for (let i = 0; i < n; i += i) {
    for (let j = 0; j < n; j++) {
      ...
    }
  }
}

在 demo2 函数中, 外层循环循环的次数 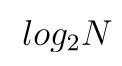, 所以其复杂度也不是 O(n^2) 而是 O(logN)。

O(logN)

如下是 二分查找 中的代码片段:

// arr 为指定数组, target 为目标元素
function binarysearch(arr, target) {
  let left = 0
  let right = arr.length - 1
  while (left <= right) {
    const middlePoint = Math.floor((left + right) / 2)
    let middle = arr[middlePoint]
    if (middle > target) {
      right = middlePoint - 1
    } else if (middle < target) {
      left = middlePoint + 1
    } else {
      return middle
    }
  }

  return '数组中目标元素不存在'
}

分析其时间复杂度。

假设数据总量为 N, 因为二分查找每次会减少一半的数据, 所以经过 1 次后, 数据剩下为 N / 2, 经过 2 次后, 数据剩下为 N / 2^2, 二分查找的极限是最后剩下 1 个数据, 假设经过 m 次后, 达到极限, N / 2^m = 1, 即 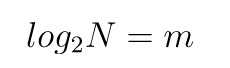, 所以时间复杂度为 logN；

题目: 现在有一个 1~1000 区间中的正整数, 需要你猜下这个数字是几, 你只能问一个问题: 大了还是小了？问需要猜几次才能猜对？

答: 根据二分查找的时间复杂度为 logN, 所以题目可以转化为求 log1000 的值, 2^10 = 1024, 所以最多猜 10 次就能猜对;

数据规模

以 JavaScript 这门语言为例, 书写如下函数

function main() {
 for (let i = 1; i <= 10; i++) {
   let n = Math.pow(10, i)
   console.time('start')
   let sum = 0
   for (let x = 0; x < n; x++) {
     sum += x
   }
   console.log(`10^${i}`)
   console.timeEnd('start')
 }
}

运行结果为:

10^1
  start: 0.14892578125ms
10^2
  start: 0.071044921875ms
10^3
  start: 0.074951171875ms
10^4
  start: 0.232177734375ms
10^5
  start: 4.281982421875ms
10^6
  start: 0.97509765625ms
10^7
  start: 8.960205078125ms
10^8
  start: 90.760986328125ms
10^9
  start: 887.587890625ms
10^10
  start: 13403.979248046875ms

可以得出如下结论:

使用 JavaScript 如果想让其在 1 s 内完成任务, 数据规模的要求如下:

• O(n^2) 算法可以处理 10^4 级别的数据;
• O(n) 算法可以处理 10^8 / 10^9 级别的数据;
• O(nlogn) 算法可以处理 10^7 数据的级别;

测试自己算法的复杂度

思路: 将数据规模乘 2, 观察对应时间的增长关系。

function testComplexity(fn) {
  for (let i = 10, i < 15, i++) {
    const total = Math.pow(2, i)
    const mockArr = new Array(total)
    console.time('test')
    /* fn 为算法函数, 这里仅仅作为 demo 演示 */
    fn(mockArr)
    console.end('test')
  }
}

递归算法的时间复杂度分析

递归中进行单次递归调用

单次递归算法的时间复杂度 = 深度 * 递归函数的时间复杂度

在单次递归算法调用中, 深度就为递归函数执行次数

/* 求 1 + 2 + 3 + ... + n */
function sum(n) {
  if (n === 0) return 0
  return n + sum(n - 1)
}

比如在 sum 函数中, 深度为 n, 递归函数的时间复杂度为 1, 所以该函数的时间复杂度为 O(n)。

递归中进行多次递归调用

递归中进行多次递归调用, 建议画图来辅助分析。

function f(n) {
  if (n === 0) return 0
  return f(n - 1) + f(n - 1)
}

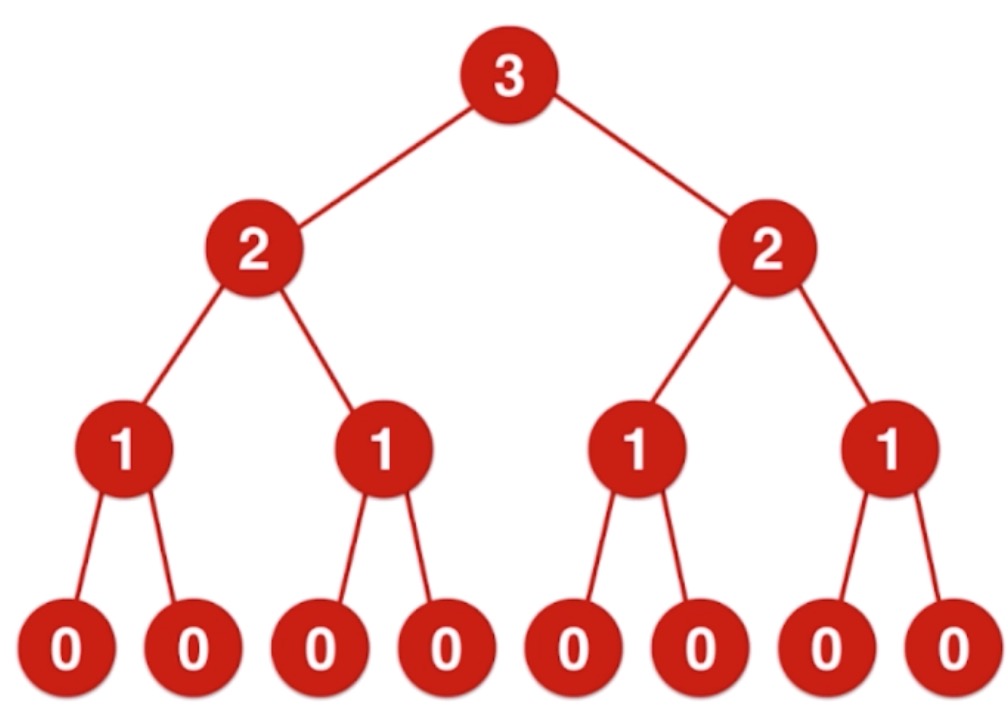
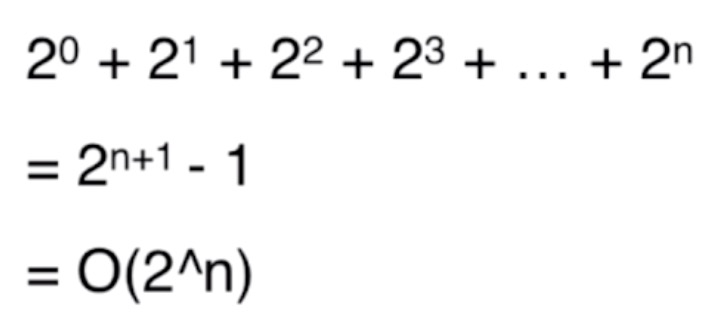
link

等差数列前 n 项和公式:

* Sn = [n*(a1+an)]/2
* Sn = a1*n + [n*(n-1)*d]/2
* Sn = d/2*n²+(a1-d/2)*n

等比数列前 n 项和公式:

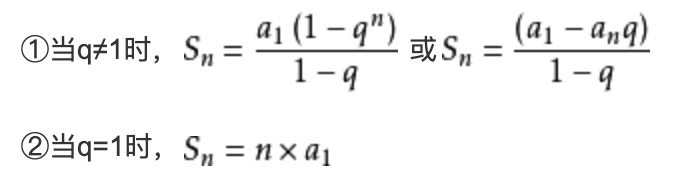
排列组合公式: