279. Perfect Squares

Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.

Example 1:

Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4

Example 2:

Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.

Analyze

题目转化: 数字 n 到 0 最少能由几个平方数相加得到?

首先思考能否使用贪心算法, 比如针对数字 12, 使用贪心算法先取能使用最大的数字 9, 结果为 9 1 1 1, 长度为 4; 但其实是有更短长度的答案 4 4 4 的, 因此不能使用贪心算法。

建模: 构建树的数据结构:

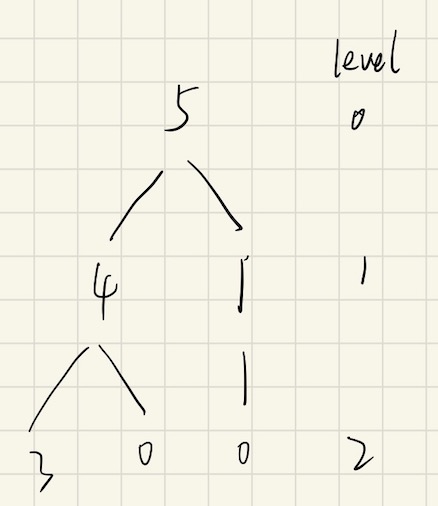
比如数字 5 到 0 的路径可以是

1. 5 -> 1 -> 0;
2. 5 -> 4 -> 0;
3. 5 -> 4 -> 3 -> 2 -> 1 -> 0;

/**
 * @param {number} n
 * @return {number}
 */
var numSquares = function(n) {
  const list = []
  list.push({ num: n, step: 0 })

  while (list.length > 0) {
    const { num, step } = list.shift()
    if (num === 0) return step
    for (let i = 1; num - i * i >= 0; i++) {
      list.push({ num: num - i * i, step: step + 1 })
    }
  }
}

此时提交代码, 运行超时。

进行分析, 以从 5 到达 1 为例, 有如下方式 ①: 5 -> 1; ②: 5 -> 4 -> 3 -> 2 -> 1; 显然不会采用第二种方式, 因此可以省略步骤二访问 1 的操作的。

使用树的数据结构时, 到达一个节点的路径是唯一确定的, 与之相对地在使用图的数据结构时, 到达一个节点的方式可能会存在多个路径; 为此引入 visitedObj 来存储该节点是否已经访问过, 改进代码如下:

/**
 * @param {number} n
 * @return {number}
 */
var numSquares = function(n) {
  const list = []
  list.push({ num: n, step: 0 })
  const visitedObj = { [n]: true }
  while (list.length > 0) {
    const { num, step, visited } = list.shift()
    for (let i = 1;; i++) {
      const extraNum = num - i * i
      if (extraNum < 0) break
      // this line return the result in advance, it reduces perform time very much.
      if (extraNum === 0) return step + 1
      if (!visitedObj[extraNum]) {
        visitedObj[extraNum] = true
        list.push({ num: num - i * i, step: step + 1 })
      }
    }
  }
}

Similar Title

127、126