图

图是一种非线性数据结构。它的表示有以下几种:

1. 邻接矩阵
2. 邻接表
3. 关联矩阵

• 邻接矩阵

邻接矩阵是表示图的常用方法, 用二维数组来表示, 数组的每个下标对应每个点。当两个点有连线则二维数组的值为 1, 否则二维数组的值为 0。但是这种表示方法会照成存储空间的浪费(因存在大量 0)。

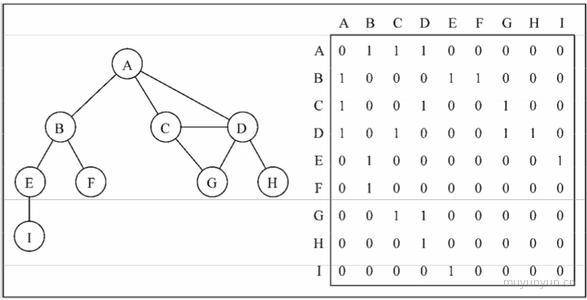
• 邻接表

如下图: 左侧为存储的顶点, 右侧为与之想对应的点, 后文会采用这种方式实现图。

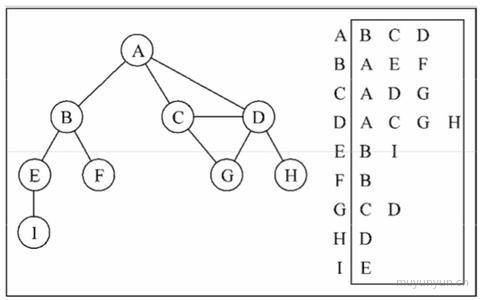
• 关联矩阵

行表示点, 列表示边。

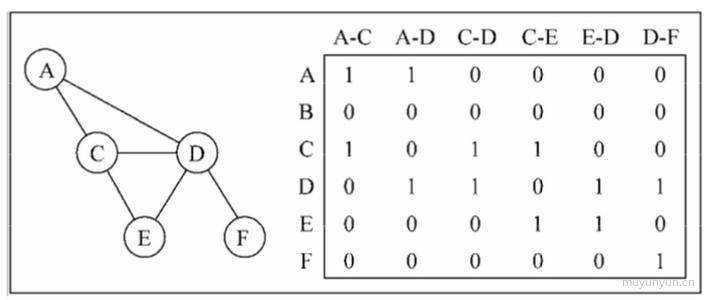
function Graph() {
  this.topPointArr = []    // 存储顶点, 笔者认为图的顶点是不会重复的
  this.edgeMap = new Map() // 存储边
}

// 往图里添加顶点
Graph.prototype.addTopPoint = function(point) {
  this.topPointArr.push(point)
  this.edgeMap.set(point, [])
}

// 往指定的点添加相邻的点
Graph.prototype.addEdge = function(point1, point2) {
  this.edgeMap.get(point1).push(point2)
  this.edgeMap.get(point2).push(point1) // 这里默认没有方向, 所以两个点互相指向
}

// 将图给打印出来
Graph.prototype.log = function() {
  let str = ''
  let neighbour
  for (let i of this.topPointArr) {
    str += i + ' -> '
    neighbour = this.edgeMap.get(i).join(' ')
    str += neighbour + '\n'
  }
  return str
}

按之前邻接表的图示, 跑如下测试用例:

var graph = new Graph()
var topArr = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
for (let i of topArr) {
  graph.addTopPoint(i)
}

graph.addEdge('A', 'B')
graph.addEdge('A', 'C')
graph.addEdge('A', 'D')
graph.addEdge('B', 'E')
graph.addEdge('B', 'F')
graph.addEdge('C', 'D')
graph.addEdge('C', 'G')
graph.addEdge('D', 'G')
graph.addEdge('D', 'H')
graph.addEdge('E', 'I')

使用自定义打印函数 graph.log(), 打印结果如下, 结果符合预期

A -> B C D
B -> A E F
C -> A D G
D -> A C G H
E -> B I
F -> B
G -> C D
H -> D
I -> E

广度优先遍历(BFS)

顾名思义, 广度优先即横向优先, 英文名为 breadth first search(BFS), 它示意图如下:

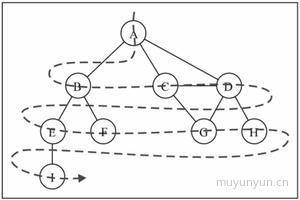
思想: 用到了队列的思想。思路如下: (标白: 未发现; 标灰: 已找寻)

• 创建队列 u, 将标灰的顶点插入队列;
• 若队列 u 不为空;
  • 从队列取出值 v;
  • 将 v 的相邻节点标灰并插入队列 u;

代码中用到队列相关的方法可参考 队列

function Queue() {
  this.items = []
}

Queue.prototype.push = function(item) {
  this.items.push(item)
}

Queue.prototype.shift = function() {
  return this.items.shift()
}

Queue.prototype.isEmpty = function() {
  return this.items.length === 0
}

Queue.prototype.size = function() {
  return this.items.length
}

Queue.prototype.clear = function() {
  this.items = []
}

Graph.prototype.bfs = function(v, callback) {
  const obj = {}

  for (let i of this.topPointArr) { // 初始化颜色
    obj[i] = 'white'
  }

  const queue = new Queue()
  obj[v] = 'gray'

  queue.push(v)

  let shiftQueue, neighbour

  while (!queue.isEmpty()) {
    shiftQueue = queue.shift()
    neighbour = this.edgeMap.get(shiftQueue)

    for (let i of neighbour) {
      if (obj[i] === 'white') {
        obj[i] = 'gray'
        queue.push(i)
      }
    }

    if (callback) {
      callback(shiftQueue)
    }
  }
}

检验完成的 bfs 函数, 进行如下调用,

graph.bfs('A', (shiftQueue) => {
  console.log(shiftQueue)
})

打印结果为 A B C D E F G H I, 符合预期。

广度优先遍历求最短路径

在上述 bfs 函数实现的基础上, 加入两个变量分别存储距离以及最短路径上先前的点

Graph.prototype.BFS = function(v) {
  const obj = {}

  const d = {}    // 新加入的变量存储距离
  const prev = {} // 新加入的变量存储最短路径上先前的点

  for (let i of this.topPointArr) { // 初始化颜色
    obj[i] = 'white'
    d[i] = 0
    prev[i] = null
  }

  const queue = new Queue()
  obj[v] = 'gray'

  queue.push(v)

  let shiftQueue, neighbour

  while (!queue.isEmpty()) {
    shiftQueue = queue.shift()
    neighbour = this.edgeMap.get(shiftQueue)

    for (let i of neighbour) {
      if (obj[i] === 'white') {
        obj[i] = 'gray'
        queue.push(i)
        d[i] = d[shiftQueue] + 1  // 这个地方卡主了~~~, 思路: 第二行的点距离第一行的点相差为 1, 第三行的点距离第二行的点相差为 1, 以此类推。
        prev[i] = shiftQueue
      }
    }
  }

  return {
    distance: d,
    prev: prev
  }
}

调用 graph.BFS('A'), 得如下结果:

{
  distance: { A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2, I: 3 }
  prev: { A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E" }
}

接下来我们处理上述返回的 prev 将最短路径打印出来:

Graph.prototype.logMinPath = function(v) {
  const { distance, prev } = this.BFS(v)
  let path = ''
  const arr = []
  Object.keys(distance).map(r => {
    path = r
    while (prev[r]) { // 终止条件为 prev 中值为 null 时
      path = prev[r] + ' - ' + path
      r = prev[r]
    }
    arr.push(path)
  })
  return arr.join('\n')
}

调用 graph.logMinPath('A'), 打印结果如下:

A
A - B
A - C
A - D
A - B - E
A - B - F
A - C - G
A - D - H
A - B - E - I

深度优先遍历(DFS)

深度优先遍历用到了栈的思想。英文名为 depth first search(DFS), 其示意图如下:

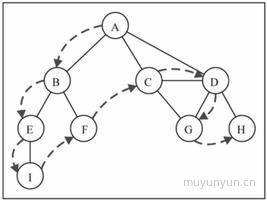
代码实现如下:

Graph.prototype.dfs = function (v, callback) {
  const obj = {}

  for (let i of this.topPointArr) { // 初始化颜色
    obj[i] = 'white'
  }

  let neighbour
  const that = this
  const find = function (v, color, cb) {
    color[v] = 'gred'
    if (cb) {
      cb(v)
    }
    neighbour = that.edgeMap.get(v)
    for (let i of neighbour) {
      if (color[i] === 'white') {
        find(i, color, cb)
      }
    }
  }

  find(v, obj, callback)
}

进行如下函数调用

graph.dfs('A', (shiftQueue) => {
  console.log(shiftQueue)  // 打印结果: A B E I F C D G H
})